THE BASICS OF
FREQUENCY STABILITY ANALYSIS
W.J. Riley, Hamilton Technical
Services
This paper reviews the basics of frequency stability analysis, and serves as a general guide to the use of the Stable32 program.
Click on the following links to go to the corresponding sections of this paper.
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
Stable32 supports the following measures of time domain frequency stability:
|
Variance Name |
Formula |
Description |
|
Allan |
s²y(t) |
Based on square of 1st differences of fractional frequency values. May use fully-overlapping samples. |
|
Modified Allan |
Mod s²y(t) |
Based on square of 1st differences of average fractional frequency values. |
|
Time |
s²x(t) |
Equal to (t²/3) · Mod Allan variance. |
|
Hadamard |
Hs²y(t) |
Based on square of 2nd differences of fractional frequency values. May use fully-overlapping samples. |
|
Total |
s²total(t) |
Uses extended data set for estimate of Allan variance with improved confidence. |
|
Modified Total |
Mod s²total(t) |
Total version of the modified Allan variance. |
|
Time Total |
Mod s²x total(t) |
Equal to (t²/3) · Mod total variance. |
|
Hadamard Total |
Hs²total(t) |
Total version of the Hadamard variance. |
These are all members of the 2-sample or Allan variance family except the Hadamard variances, which are 3-sample variances.
The most common time domain stability measure is the Allan variance (AVAR), s²y(t), which gives a value for the fractional frequency fluctuations as a function of averaging time, t. The other common time domain statistics are the modified Allan variance (MVAR), Mod s²y(t) and the time variance, s²x(t). The modified Allan variance is better able to distinguish between white and flicker phase noise. The time variance (TVAR), s²x(t) measures the time fluctuations of a source or time distribution system. All of these quantities are usually expressed as their square roots ADEV, sy(t), MDEV, Mod sy(t) and TDEV, sx(t). They are dimensionless except for the latter, which has units of seconds.
The Allan variance can be estimated by either the normal, overlapping or total method. The latter two methods provide better statistical confidence at the expense of increased computational time. The results can be shown for a single t, over a range of octave or decade t spacings, or at every t for which there is sufficient data.
The Hadamard variance is a 3-sample variance that is similar to the 2-sample Allan variance. It examines the 2nd difference of the fractional frequencies, the 3rd difference of the phase variations. Because of this, the Hadamard variance, HVAR or Hs²y(t), converges for the flicker walk FM (a = -3) and random run FM (a = -4) power-law noise types. It is also unaffected by linear frequency drift.
ALLAN VARIANCE
The normal Allan, or 2-sample variance, AVAR, is the most common time domain measure of frequency stability. It is defined as:
|
|
1 |
M-1 |
|
|
s²y(t)= |
¾¾¾¾ |
S |
[ y(i+1) - y(i) ]², |
|
|
2(M-1) |
i=1 |
|
where y(i) is the ith of M fractional frequency values averaged over the measurement interval t. In terms of phase data, the Allan variance may be calculated as:
|
|
1 |
N-2 |
|
|
s²y(t) = |
¾¾¾¾ |
S |
[ x(i+2) - 2x(i+1) + x(i) ]², |
|
|
2(N-2)t² |
i=1 |
|
where x(i) is the ith of the N = M+1 phase values spaced by the measurement interval t.
The result is usually expressed as the square root, sy(t), the Allan deviation, ADEV. The Allan variance is the same as the ordinary variance for white FM noise, but has the advantage, for more divergent noise types such as flicker FM noise, of converging to a value that is not dependent on the number of samples. The confidence interval of an Allan deviation estimate is dependent on the noise type, but is often approximated as ±sy(t)/ÖN.
The overlapping Allan variance is a form of the normal Allan variance, s²y(t), AVAR, that makes maximum use of a data set by forming all possible fully overlapping samples at each averaging time t. It can be estimated from a set of M frequency measurements for averaging time t = mt0, where m is the averaging factor and t0 is the basic measurement interval, by the expression:
|
|
1 |
M-2m+1 |
j+m-1 |
|
|
s²y(t) = |
¾¾¾¾¾¾ |
S |
{ S |
[ y(i+m) - y(i) ] }². |
|
|
2m²(M-2m+1) |
j=1 |
i=j |
|
In terms of phase data, the overlapping Allan variance can be estimated from a set of N = M+1 time measurements as:
|
|
1 |
N-2m |
|
|
s²y(t) = |
¾¾¾¾¾ |
S |
[ x(i+2m) - 2x(i+m) + x(i) ] }². |
|
|
2t²(N-2m) |
i=1 |
|
The result is usually expressed as the square root, sy(t), the Allan deviation, ADEV. The confidence interval of an overlapping Allan deviation estimate is better than that of a normal Allan variance estimation because, even though the additional overlapping differences are not statistically independent, they nevertheless increase the number of degrees of freedom and thus improve the confidence in the estimation.
The modified Allan variance, Mod s²y(t), MVAR, is another common time domain measure of frequency stability. It is estimated from a set of M frequency measurements for averaging time t=mt0, where m is the averaging factor and t0 is the basic measurement interval, by the expression:
|
|
1 |
M-3m+2 |
j+m-1 |
i+m-1 |
|
|
Mod s²y(t) = |
¾¾¾¾¾¾ |
S |
{ S |
S |
[y(k+m) - y(k) ] }². |
|
|
2m4 (M-3m+2) |
j=1 |
i=j |
k=i |
|
In terms of phase data, the modified Allan variance is estimated from a set of N = M+1 time measurements as:
|
|
1 |
N-3m+1 |
j+m-1 |
|
|
Mod s²y(t) = |
¾¾¾¾¾¾ |
S |
{ S |
[x(i+2m) -2x(i+m) + x(i) ] }². |
|
|
2m²t²(N-3m+1) |
j=1 |
i=j |
|
The result is usually expressed as the square root, Mod sy(t), the modified Allan deviation. The modified Allan variance is the same as the normal Allan variance for m = 1. It includes an additional averaging operation, and has the advantage of being able to distinguish between white and flicker PM noise.
The time variance, TVAR, is a measure of time stability based on the modified Allan variance. It is defined as:
s²x(t) = (t²/3)·Mod s²y(t).
The time variance is equal to the standard variance of the time deviations for white PM noise. Its square root, TDEV, is particularly useful for measuring the stability of a time distribution network.
The Hadamard variance is a 3-sample variance that is similar to the 2-sample Allan variance. It examines the 2nd difference of the fractional frequencies, the 3rd difference of the phase variations. Because of this, the Hadamard variance, HVAR or Hs²y(t), converges for the flicker walk (a = -3) and random run (a = -4) FM power-law noise types. It is also unaffected by linear frequency drift.
For frequency data, the Hadamard variance is defined as:
|
|
1 |
M-2 |
|
|
Hs²y(t) = |
¾¾¾¾ |
S |
[ y(i+2) -2y(i+1) + y(i) ]², |
|
|
6(M-2) |
i=1 |
|
where y(i) is the ith of M fractional frequency values at averaging time t.
For phase data, the Hadamard variance is defined as:
|
|
1 |
N-3 |
|
|
Hs²y(t) = |
¾¾¾¾ |
S |
[ x(i+3) - 3x(i+2) + 3x(i+1) - x(i) ]², |
|
|
6t²(N-3 ) |
i=1 |
|
where x(i) is the ith of N = M+1 phase values at averaging time t.
Like the Allan variance, the Hadamard variance is usually expressed as its square-root, the Hadamard deviation, HDEV or Hsy(t). The Hadamard variance is equal to the Allan variance if the data has no frequency drift. It is particularly useful for measuring the stability of a frequency source having frequency drift or highly-divergent noise.
The overlapping Allan variance is a form of the Hadamard variance, Hs²y(t), HVAR, that makes maximum use of a data set by forming all possible fully overlapping samples at each averaging time t. It can be estimated from a set of M frequency measurements for averaging time t = mt0, where m is the averaging factor and t0 is the basic measurement interval, by the expression:
|
|
1 |
M-3m+1 |
j+m-1 |
|
|
Hs²y(t) = |
¾¾¾¾¾¾ |
S |
{ S |
[y(i+2m) -2y(i+m) + y(i) ] }², |
|
|
6m²(M-3m+1) |
j=1 |
i=j |
|
where y(i) is the ith of M fractional frequency values at averaging time t.
For phase data, the overlapping Hadamard variance is defined as:
|
|
1 |
N-3m |
|
|
Hs²y(t) = |
¾¾¾¾ |
S |
[ x(i+3m) - 3x(i+2m) + 3x(i+m) - x(i) ]², |
|
|
6t²(N-3m ) |
i=1 |
|
where x(i) is the ith of N = M+1 phase values at averaging time t.
The total variance, TOTVAR, is a relatively new statistic that extends the measured data by double-sided reflection to reduce the estimation error for long averaging factors. The total variance is defined for phase data as:
|
|
1 |
N-1 |
|
|
s²total(t) = |
¾¾¾ |
S |
[ x*(i-m) -2x*(i)+x*(i+m) ]² , |
|
|
2t²(N-2) |
i=2 |
|
where t = mt0, and the N phase values x(i) measured at t = t0 are extended by reflection about both endpoints to form a virtual sequence x*.
The result is usually expressed as the square root, stotal(t), the total deviation, TOTDEV. The expected value of TOTVAR is the same as AVAR for white and flicker PM noise and white FM noise. Bias corrections need to be applied for flicker and random walk FM noise.
The modified total variance, MTOT, is total version of the modified Allan variance. It is defined for phase data as:
|
|
1 |
N-3m+1 |
1 |
N+3m-1 |
|
|
Mod s²total(t) = |
¾¾¾¾¾¾¾ |
S |
¾ |
S |
[0zi*(m)]², |
|
|
2m²t0²(N-3m+1) |
n=1 |
6m |
i=n-3m |
|
where the 0zi*(m) terms are the phase averages from a triply-extended sequence created by uninverted even reflection at each end, and the prefix 0 denotes that the linear trend has been removed.
The time total variance, TTOT, is simply the modified total variance scaled by (t²/3).
The Hadamard total variance, HTOT, is a total version of the Hadamard variance that offers improved confidence at large averaging factors. It is defined as:
|
|
1 |
N-3m+1 |
1 |
n+3m-1 |
|
|
Total Hs²y(t) = |
¾¾¾¾¾ |
S |
{ ¾ |
S |
[Hi(m)]² }, |
|
|
6(N-3M-1) |
n=1 |
6m |
i=n-3m |
|
Where the Hi(m) terms are Hadamard 2nd differences from triply-extended, drift-removed subsequences.
Stable32 uses several methods for setting the confidence intervals and error bars for its stability analysis and plotting functions. The confidence interval of a variance estimate depends not only on the variance type and nominal value, and on the averaging factor and number of data points, but also on the statistical confidence factor desired and the dominant noise type.
The simplest confidence interval approximation, with no consideration of the noise type, sets the ±1s (68%) error bars at ±sy(t)/ÖN, where N is the number of frequency data points used to calculate the Allan deviation. A more accurate determination of this confidence interval can be made by considering the noise type, which can be estimated by the B1 bias function (the ratio of the standard variance to the Allan variance). That noise type is then be used to determine a multiplicative factor, Kn, to apply to the confidence interval:
|
NoiseType |
Kn |
|
Random Walk FM |
0.75 |
|
Flicker FM |
0.77 |
|
White FM |
0.87 |
|
Flicker PM |
0.99 |
|
White PM |
0.99 |
Better statistical confidence can be obtained by making maximum use of the available data by forming all possible frequency differences for a given averaging time. Although these fully overlapping samples are not all statistically independent, they nevertheless help to improve the confidence of the resulting Allan deviation estimate. Furthermore, Chi-squared statistics can be applied to calculate single and double-sided confidence intervals at any desired confidence factor, based on a determination of the number of degrees of freedom for the estimated noise type. The error bars are then determined by Chi-squared statistics, using the equivalent number of freedom for the particular noise type, averaging factor, and number of data points.
Analytical methods are available for calculating the equivalent number of degrees of freedom for the various variance estimations, and using that to establish single or double-sided confidence intervals for the estimate with a certain confidence factor, based on Chi-squared statistics.
Sample variances are distributed according to the expression:
|
|
df · s² |
|
c² = |
¾¾¾ , |
|
|
s² |
where c² is the Chi-square, s² is the sample variance, s² is the true variance, and df is the number of degrees of freedom (not necessarily an integer). The df is determined by the number of data points and the noise type. The Stable32 program includes procedures for setting these confidence limits.
During the Run function, noise type estimates are made at each averaging factor . The # in the Run stability table, and the # Analysis Pts in the detailed Sigma dialog box, is the number of analysis points (the # of 2nd or 3rd differences summed) in the sigma calculation. This number is used in determining the confidence intervals. Without gaps, the #s are equal to the following:
|
Sigma Type |
# |
|
Normal Allan |
M/m –1 |
|
Overlapping Allan |
M-2m+1 = N-2m |
|
Modified Allan & Time |
M-3m+2 = N-3m+1 |
|
Hadamard |
M/m –2 |
|
Overlapping Hadamard |
M-3m+1 = N-3m |
|
Total |
M-m = N-m-1 |
|
Modified Total |
M-3m+2 = N-3m+1 |
|
Hadamard Total |
M-3m+1 = N-3m |
where: N = # phase data points = M+1, M = # frequency data points and m = AF = averaging factor
For the normal Allan and Hadamard variances, the rounding down associated with successive averaging may reduce the #. With gaps, the # can depend on exactly where the gaps are. In all cases, the # is counted dynamically during the calculation as the statistical sums are accumulated.
Several bias functions are defined and used in the analysis of frequency stability. These bias functions are defined below. The Stable32 program uses the B1, the standard variance to Allan variance ratio, and R(n), the modified Allan variance to normal Allan variance ratio bias functions for the identification of noise types.
The B1 bias function is the ratio of the N-sample (standard) variance to the 2-sample (Allan) variance with dead time ratio r = T/t, where T = time between measurements, t=averaging time, and m=exponent of t in Allan variance for a certain power law noise process:
|
|
s²(N, T, t) |
|
B1(N, r , m) = |
¾¾¾¾ . |
|
|
s²(2, T, t) |
The B2 bias function is the ratio of the 2-sample (Allan) variance with dead time ratio r = T/t to the 2-sample (Allan) variance without dead time (r = 1):
|
|
s²(2, T, t) |
|
B2(r , m) = |
¾¾¾¾ . |
|
|
s²(2, t, t) |
The B3 bias function is the ratio of the N-sample (standard) variance with dead time ratio r = T/t at multiples M = t/t0 of the basic averaging time t0 to the N-sample variance with the same dead time ratio at averaging time t:
|
|
s²(N, M, T, t) |
|
B3(N, M, r , m) = |
¾¾¾¾¾ . |
|
|
s²(N, T, t) |
The R(n) function is the ratio of the modified Allan variance to the normal Allan variance for n = # phase data points. Note: R(n) is also a function of a, the exponent of the power law noise type:
|
|
Mod s²y(t) |
|
R(n) = |
¾¾¾¾ . |
|
|
s²y(t) |
The TOTVAR statistic is an unbiased estimator of the Allan variance for white and flicker PM noise, and for white FM noise. For flicker and random walk FM noise, TOTVAR is biased low as t becomes significant compared with the record length. The ratio of the expected value of TOTVAR to AVAR is given by the expression:
B(TOTAL) = 1 - c×t/(T- t)
where c = 1/6× ln2 = 0.240 for flicker FM noise, c = 3/8 = 0.375 for random walk FM noise, and T is the record length. At the maximum allowable value of t = T/2, TOTVAR is biased low by about 26% for RW FM noise.
Similar bias functions apply to the MTOT and HTOT statistics. The Stable32 program applies those bias functions automatically as required to correct the reported results.
Stable32 uses the following frequency domain measures of frequency stability:
|
Formula |
Units |
Description |
|
Sy(f) |
1/Hz |
PSD of fractional frequency fluctuations |
|
Sx(f) |
sec²/Hz |
PSD of time fluctuations |
|
Sf(f) |
rad²/Hz |
PSD of phase fluctuations |
|
£(f) |
dBc/Hz |
SSB phase noise to carrier power ratio |
where: PSD = Power Spectral Density, SSB = Single Sideband and dBc = Decibels with respect to carrier power.
The most common frequency domain stability measure is £(f), dBc/Hz, the SSB phase noise to signal ratio in a 1 Hz BW as a function of sideband frequency, f. Other frequency domain stability measures are: Sy(f), 1/Hz, the power spectral density of the fractional frequency fluctuations; Sx(f), sec²/Hz, the power spectral density of the time fluctuations; and Sf(f), rad²/Hz, the power spectral density of the phase fluctuations. The Stable32 program can plot any of these from the appropriate phase or frequency data.
The spectral characteristics of the power law noise processes commonly used to describe the performance of frequency sources are shown in the following table:
|
Noise Type |
a |
b |
m |
m¢ |
h |
|
White PM |
2 |
0 |
-2 |
-3 |
-1 |
|
Flicker PM |
1 |
-1 |
-2 |
-2 |
0 |
|
White FM |
0 |
-2 |
-1 |
-1 |
1 |
|
Flicker FM |
-1 |
-3 |
0 |
0 |
2 |
|
Random Walk FM |
-2 |
-4 |
1 |
1 |
3 |
|
Flicker Walk FM |
-3 |
-5 |
2 |
2 |
4 |
|
Random Run FM |
-4 |
-6 |
3 |
3 |
5 |
Four types of power spectral density (PSD) are commonly used to describe the stability of a frequency source:
- PSD of Frequency Fluctuations Sy(f): The power spectral density (PSD) of the fractional frequency fluctuations y(t) in units of 1/Hz is given by Sy(f) = h(a) ·f a, where f = sideband frequency, Hz.
- PSD of Phase Fluctuations Sf(f): The PSD of the phase fluctuations in units of rad²/Hz is given by Sf(f) = (2pn0)² · Sx(f), where n0 = carrier frequency, Hz.
- PSD of Time Fluctuations Sx(f): The PSD of the time fluctuations x(t) in units of sec²/Hz is given by Sx(f) = h(b) · f b = Sy(f)/(2pf)², where: b = a-2. The time fluctuations are related to the phase fluctuations by x(t) = f(t)/2pn0. Both are commonly called "phase" to distinguish them from the independent time variable, t. Stable32 uses x(t) and y(t) arrays as its phase and frequency variables.
- SSB Phase Noise £(f): The SSB phase noise in units of dBc/Hz is given by £(f) = 10 · log[½ · Sf(f)]. This is the most common engineering units to specify phase noise.
Six types of variance are commonly used to describe the stability of a frequency source:
- Standard Variance s²(t): The N-sample or standard variance is not recommended as a general-purpose measure of frequency stability because it is not convergent for some types of noise commonly found in frequency sources. It is used primarily in the calculation of the B1 ratio for noise recognition.
- Allan Variance s²y(t): The Allan variance is given by s²y(t) = A(m) · tm, where t = averaging time, seconds. It is the most common measure of the fluctuations of the fractional frequency y(t) = [n(t)-n0]/n0 = Dn/n0 = x'(t).
- Modified Allan Variance s²y(t): The modified Allan variance is given by Mod s²y(t) = B(m) · tm', where m' =-a-1.
- Time Variance s²x(t): The time variance in units of seconds is given by s²x(t) = C(h) · th =(t²/3) · Mod s²y(t), sec, where h = b-1.
- Hadamard Variance Hs²y(t): The 3-sample (Hadamard) variance is used primarily as an alternative to the Allan variance for a frequency source having linear frequency drift or highly-divergent noise.
- Total Variances: Total versions of the Allan, modified Allan, time, and Hadamard variances use extended data to provide improved confidence at large averaging factors.
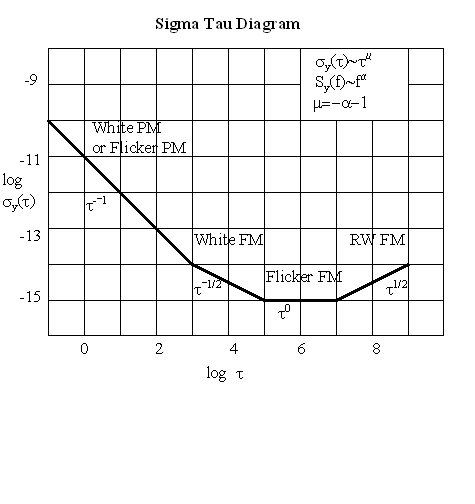
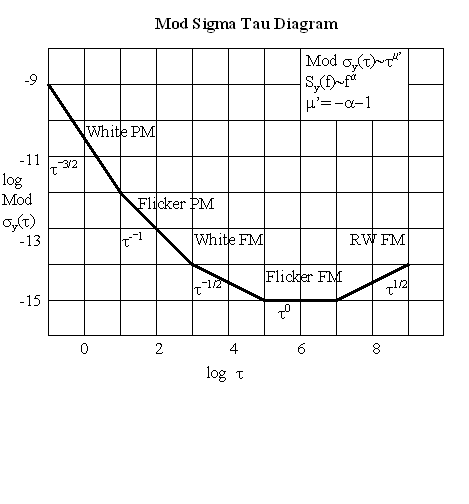
The following two diagrams show the relationship between the log s versus log t slopes for various power law noise processes for the normal and modified Allan variances. Note that Mod sy(t) is able to distinguish between white and flicker PM noise.
NOISE SPECTRA
The random phase and frequency fluctuations of a frequency source can be modeled by power law spectral densities of the form:
Sy(f) = h(a)f a
where: Sy(f) = one-sided power spectral density of thefractional frequency fluctuations, 1/Hz, f = Fourier or sideband frequency, Hz, h(a) = intensity coefficient, and a = exponent of the power law noise process.
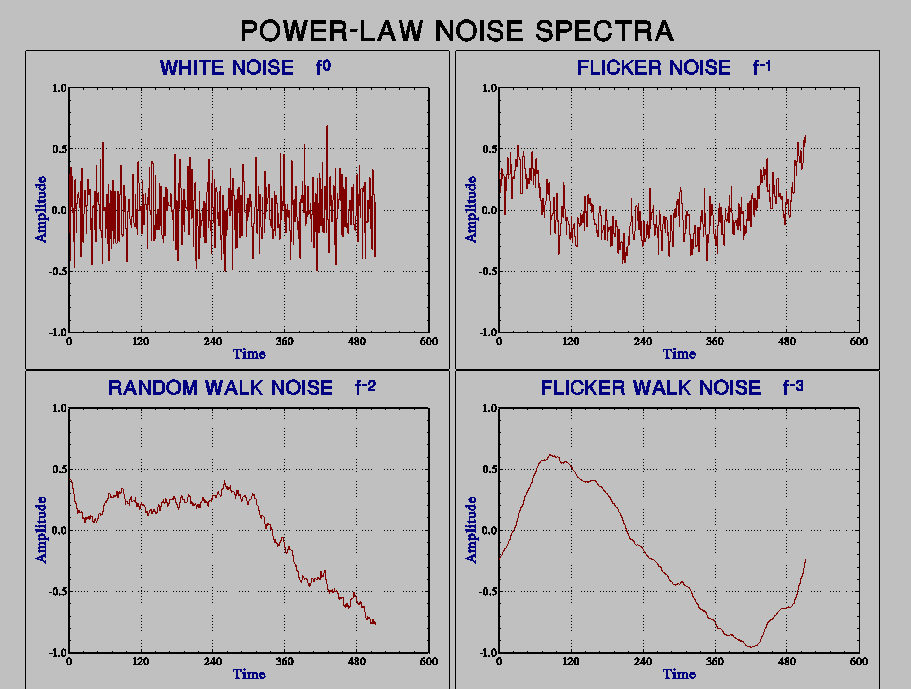
The most commonly encountered noise spectra are white (f 0), random walk (f -2), flicker (f -1),and flicker walk (f -3). Examples showing the appearance of these noise types are shown below.
Spectral models can be applied to both phase and frequency power spectral densities (PSD). Phase is the time integral of frequency, so the relationship between them is as 1/f²: Sx(f) = Sy(f)/(2pf)² where: Sx(f) = PSD of the time fluctuations, sec²/Hz.
Two other quantities are also commonly used to measure phase noise, Sf(f) = PSD of the phase fluctuations, rad²/Hz and its logarithmic equivalent £(f), dBc/Hz. The relationship between these is: Sf(f) = (2pn0)² · Sx(f) and £(f) = 10 · log[½ · Sf(f)], where n0 is the carrier frequency, Hz. The power law exponent of the phase noise power spectral densities is b =a-2. These frequency-domain power law exponents are also related to the slopes of the following time domain stability measures:
|
Variance |
Equation |
Noise Exponent |
|
Allan, Total, Hadamard, Total Hadamard |
s²y(t), etc. |
m = a-1, a<2 |
|
Modified Allan, Modified Total |
Mod s²y(t), etc. |
m' = a-1, a<3 |
|
Time, Time Total |
s²x(t), etc. |
h = a-1, a<3 |
The stability of a frequency source can be specified and measured in either the time or frequency domain. Examples of these stability measures are the Allan variance, s²y(t), in the time domain and the spectral density of the fractional frequency fluctuations, Sy(f), in the frequency domain. Conversions between these domains may be made by an analytical method based on a power law spectral model for the noise processes involved. This method, the one used by the Stable32 Domain function, can be applied only when the dominant noise process decreases toward higher sideband frequencies. Otherwise a more fundamental method based on numerical integration must be used. The general time to frequency domain conversion is not unique because white and flicker phase noise have the same Allan variance t dependence. When performing any of these conversions, it is necessary to choose a reasonable range for s and t in the domain being converted to. The main lobe of the sy(t) and Mod sy(t) responses occur at the Fourier frequency f = 1/2t.
Domain conversions may be made for power law noise models by using the following conversion formulae:
|
Noise Type |
s²y(t) |
Sy(f) |
|
RW FM |
A · f 2 · Sy(f) · t 1 |
A-1 · t -1 · s²y(t) · f -2 |
|
F FM |
B · f 1 · Sy(f) · t 0 |
B-1 · t 0 · s²y(t) · f -1 |
|
W FM |
C · f 0 · Sy(f) · t -1 |
C-1 · t 1 · s²y(t) · f 0 |
|
F PM |
D · f -1 · Sy(f) · t -2 |
D-1 · t 2 · s²y(t) · f 1 |
|
W PM |
E · f -2 · Sy(f) · t -2 |
E-1 · t 2 · s²y(t) · f 2 |
where: A = 4p²/6, B = 2·ln2, C = 1/2, D = 1.038 + 3·ln(2pfht0)/4p², E = 3fh /4p² and fh is the upper cutoff frequency of the measuring system in Hz, and t0 is the basic measurement time. This factor applies only to white and flicker PM noise.
Stable32 uses the median absolute deviation (MAD) as its means of outlier recognition. The MAD is a robust statistic based of the median of the data. It is the median of the scaled absolute deviations of the data points from their median value, and is defined as:
MAD = Median { | y(i) - m | / 0.6745 }
where m = Median { y(i) }, and the factor 0.6745 makes the MAD equal to the standard deviation for normally distributed data. Each frequency data point, y(i), is compared with the median value of the data set, m, plus or minus the desired multiple of the MAD. Judgment is required when removing outliers. Automatic outlier removal is convenient for quickly plotting and analyzing frequency data, which may have to be removed to obtain meaningful results. It also provides a certain degree of objectivity. But the analyst is still responsible for decisions regarding outlier removal. It is particularly important to explain all phase discontinuities.
Several drift analysis methods are available for both phase or frequency data as described below. The best method depends on the degree that the resulting drift model fits the data, which can be judged by the randomness of the residuals.
|
Data |
Method |
Noise Model |
|
Phase |
Quadratic Fit |
W PM |
|
Phase |
Avg of 2nd Diffs |
RW FM |
|
Phase |
3-Point Fit |
W & RW FM |
|
Phase |
Linear |
Frequency Offset |
|
Phase |
Endpoints |
Frequency Offset |
|
Freq |
Linear Fit |
W FM |
|
Freq |
Bisection Fit |
W & RW FM |
|
Freq |
Log Fit |
Stabilization |
|
Freq |
Diffusion Fit |
Diffusion |
Three drift methods are available to analyze frequency drift in phase data:
- Quadratic Fit: The first is a least-squares quadratic fit to the phase data, x(t) = a + bt + ct², where y(t) = x'(t) = b + 2ct, slope = y'(t) = 2c. This method is optimum for white PM noise. It is the default, and is also the method used for drift analysis when plotting phase data.
- 2nd Differences: The second method is the average of the 2nd differences of the phase data, y(t) = [x(t+t)-x(t)]/t, slope = [y(t+t)-y(t) ]/t = [ x(t+2t)-2x(t+t)+x(t)]/t².This method is optimum for random walk FM noise.
- 3-Point: The third method uses the 3 points at the start, middle and end of the phase data, slope = 4[x(end)-2x(mid)+x(start)]/(Mt)², where M = # data points It is the equivalent of the bisection method for frequency data.
Frequency offset may be calculated in phase data by either of two methods:
- Linear Fit: The first (optimum for white PM noise) uses a least-squares linear fit to the phase data, x(t) = a + bt, where slope = y(t) = b.
- Endpoints: The second method simply uses the difference between the first and last points of the phase data, slope = y(t) = [ x(end) - x(start) ] / (M-1), where M = # phase data points. This method is used mainly to match the two endpoints.
Four drift methods are also available for frequency data:
- Linear Fit: The first, the default, is a least squares linear regression to the frequency data, y(t) = a+bt, where a = intercept, b = slope = y'(t). This is the optimum method for white FM noise.
- Bisection: The second method computes the drift from the frequency averages over the first and last halves of the data, slope = 2 [ y(2nd half) - y(1st half) ] / (Nt), where N = # points. This bisection method is optimum for white and random walk FM noise.
- Log Fit: The third method, a log model of the form (see MIL-O-55310B), y(t) = a·ln(bt+1), where slope = y'(t) = ab/(bt+1) which applies to frequency stabilization.
- Diffusion Fit: The last frequency drift method is a diffusion (Ö t) model of the form y(t) = a+b(t+c)1/2, where slope=y'(t)=½·b(t+c)-1/2.
The normal Allan variance function calculates sy(t) and the standard deviation, and uses their ratio to estimate the noise type and the confidence interval of the Allan deviation.
The overlapping Allan variance function also calculates and displays sy(t). It also estimates the noise type, and uses that to determine the # of degrees of freedom. It then establishes single or double-sided confidence intervals for the Allan deviation based on a certain confidence factor.
The modified Allan variance function requests the averaging factor and bandwidth factor for the measuring system, BW = 2pfht0, where fh is the upper cutoff frequency in Hz. It then calculates sy(t) and Mod sy(t), and uses their ratio to estimate the noise type. This function then continues with the determination of single or double-sided confidence intervals for the modified Allan deviation for the estimated noise type and desired confidence factor.
The Hadamard variance uses 3 (rather than 2) fractional frequency samples, which allows it to converge for a = -3 (Flicker Walk FM) and a = -4 (Random Run FM) noises, and causes it to be unaffected by linear frequency drift.
The total variance uses extended data to form a statistic that provides a better estimate for sy(t) at long averaging times. See the Total Variance help screen for more information about this new time-domain stability measure.
Total versions of the modified Allan, time and Hadamard variances are also supported.
The type of power law noise is estimated for most of the variance types by using either the B1 ratio (the ratio of the standard variance to the Allan variance for zero dead time) or R(n) (the ratio of the modified to normal Allan variances) as shown in the following table. The bandwidth factor BW=2pfht0 (where fh is the measuring system bandwidth in Hz) applies to the R(n) calculation for flicker PM noise.
Single or double-sided confidence intervals are determined using the # of analysis points, estimated noise type and method shown in the following table. These are then used to calculate the corresponding maximum (and optionally) minimum sigma values.
|
Variance |
Noise Estimation Method |
CI Method |
|
Normal Allan |
B1 Ratio |
Kn factor |
|
Overlapping Allan |
B1 Ratio |
c² statistics |
|
Modified Allan |
B1 & R(n) Ratios |
c² statistics |
|
Time |
B1 & R(n) Ratios |
c² statistics |
|
Hadamard |
None |
None |
|
Overlapping Hadamard |
*B1 Ratio |
c² statistics |
|
Total |
B1 Ratio |
c² statistics (df +1) |
|
Modified Total |
B1 & R(n) Ratios |
c² statistics |
|
Time Total |
B1 & R(n) Ratios |
c² statistics |
|
Total Hadamard |
*B1 Ratio |
c² statistics |
The following terms are used in the field of frequency stability analysis and the Stable32 program
- Aging The change in frequency with time due to internal effects within the device.
- Allan Variance The 2-sample variance s²y(t) commonly used to measure frequency stability.
- BW Bandwidth, Hz.
- Confidence Limit The uncertainty associated with a measurement. Often a 68% confidence level or error bar.
- Drift The change in frequency with time due to all effects (including aging and environmental sensitivity).
- Hadamard Variance A 3-sample variance, HVAR, that is similar to the 2-sample Allan variance. It uses the 2nd differences of the fractional frequencies, and is unaffected by linear frequency drift.
- £(f) The ratio of the SSB phase noise power in a 1 Hz BW to the total carrier power, dBc/Hz.
- MJD The Modified Julian Date is based on the astronomical Julian Date, the # of days since noon on January 1, 4713 BC. The MJD is the Julian Date - 2,4000,000.5
- Normalize To remove the average value from phase or frequency data .
- Phase Noise The spectral density of the phase deviations.
- Sigma The square root or deviation of a variance, often the 2-sample or Allan deviation, sy(t).
- Slope The change in frequency per tau interval.
- SSB Single sideband.
- Sf(f) The one-sided spectral density of the phase deviations, rad²/Hz.
- Sx(f) The one-sided spectral density of the time deviations, sec²/Hz.
- Sy(f) The one-sided spectral density of the fractional frequency deviations, 1/Hz.
- Total Variance A statistic that provides improved confidence by extending the data set to increase the number of equivalent degrees of freedom.
- Tau The interval between phase measurements or the averaging time used for a frequency measurement.
- x(t) The instantaneous time deviation from a nominal time, x(t) = f(t)/2pn0, seconds, where n0 is the nominal frequency, Hz. This dependent time variable is often called "phase" to distinguish it from the independent time variable t.
- y(t) The instantaneous fractional frequency deviation from a nominal frequency, y(t) = [n(t)-n0]/n0] = x'(t), where n0 is the nominal frequency.
The following references are recommended to support the use of the Stable32 program for the analysis of frequency stability:
- "Characterization of Clocks and Oscillators", NIST Technical Note1337, D. B. Sullivan, D.W. Allan, D.A. Howe and F. L. Walls, Eds., U.S. Dept. of Commerce, National Institute of Standards and Technology, March 1990.
- S.R. Stein, "Frequency and Time-Their Measurement and Characterization", Chap. 12, Precision Frequency Control, E.A. Gerber and A. Ballato, Eds., Academic Press, Inc., Orlando, 1985, ISBN 0-12-280602-6 (Vol. 2).
- D.W. Allan, "Statistics of Atomic Frequency Standards", Proc. IEEE, Vol. 54, pp. 221-230, Feb. 1966.
- J.A. Barnes, et al, "Characterization of Frequency Stability", IEEETrans. Instrum. Meas., Vol. IM-20, No. 2, pp. 105-120, May 1971.
- D.A. Howe, D.W. Allan and J.A. Barnes, "Properties of Signal Sources and Measurement Methods", Proc. 35th Annu. Freq. Control Symp., pp. A1-A47, June, 1981.
- Report 580, "Characterization of Frequency and Phase Noise", International Radio Consultative Committee (C.C.I.R.), pp. 142-150, 1986.
- J.A. Barnes, "The Analysis of Frequency and Time Data", Austron, Inc., Dec. 1991.
- D.W. Allan, et al., " Standard Terminology for Fundamental Frequency and Time Metrology", Proc. 42nd Annu. Freq. Control Symp., pp. 419-425, June, 1988.
- W.J. Riley, "A Test Suite for the Calculation of Time Domain Frequency Stability", Proc. 1995 IEEE Freq. Contrl. Symp., pp. 360-366, June 1995.
- W.J. Riley, "Addendum to a Test Suite for the Calculation of Time Domain Frequency Stability", Proc. 1996 IEEE Freq. Contrl. Symp., pp. 880-882, June 1996.
- "IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology," IEEE Std. 1139-1988.
- J.A. Barnes, "The Measurement of Linear Frequency Drift in Oscillators", Proc. 15th Annu. PTTI Meeting, pp. 551-582, Dec. 1983.
- M.A. Weiss and C. Hackman, "Confidence on the Three-Point Estimator of Frequency Drift", Proc. 24th Annu. PTTI Meeting, pp. 451-460, Dec. 1992.
- MIL-PRF-55310, Oscillators, Crystal, General Specification For.
- D.W. Allan and J.A. Barnes, "A Modified Allan Variance with Increased Oscillator Characterization Ability", Proc. 35th Annu. Symp. on Freq. Contrl., pp. 470-474, May 1981.
- D.W. Allan, D.D. Davis, J. Levine, M.A. Weiss, N. Hironaka, and D. Okayama, " A New Inexpensive Frequency Calibration Service From NIST ", Proc. 44th Annu. Symp. on Freq. Contrl., pp. 107-116, June 1990.
- D.W. Allan, M.A. Weiss, and J.L. Jespersen, "A Frequency-Domain View of Time-Domain Characterization of Clocks and Time and Frequency Distribution Systems", Proc. 45th Annu. Symp. on Freq. Contrl., pp. 667-678, May 1991.
- D.W. Allan, "Time and Frequency Metrology: Current Status and Future Considerations", Proc. 5th European Freq. and Time Forum, pp. 1-9, March 1991.
- C.A. Greenhall, "A Shortcut for Computing the Modified Allan Variance", Proc. 1992 IEEE Freq. Contrl. Symp., pp. 262-264, May 1992.
- B.E. Blair (Editor), Time and Frequency: Theory and Fundamentals, NBS Monograph 140, Annex 8.E, p. 181, May 1974.
- S.K. Park and K.W. Miller, "Random Number Generators: Good Ones are Hard to Find", Comm. ACM, Vol. 31, No. 10, pp. 1192-1201, Oct. 1988.
- W.H. Press, B.P. Flannery, S.A. Teukolsky and W.T. Vetterling, Numerical Recipes in C, Cambridge Univ. Press, Cambridge, U.K., 1988, pp. 216-217.
- D.B. Percival, "Use of Robust Statistical Techniques in Time Scale Formation", Preliminary Report, U.S. Naval Observatory Contract No. N70092-82-M-0579, 1982.
- Gernot M.R. Winkler, "Introduction to Robust Statistics and Data Filtering", Tutorial at 1993 IEEE Freq. Contrl. Symp., Sessions 3D and 4D, June 1, 1993.
- C.A. Greenhall, "Recipes for Degrees of Freedom of Frequency Stability Estimators", IEEE Trans. Instrum. Meas., Vol. 40, No. 6, pp. 994-999, Dec. 1991.
- C.A. Greenhall, "Estimating the Modified Allan Variance", Proc. IEEE 1995 Freq. Contrl. Symp., pp. 346-353, June 1995.
- N.J. Kasdin and T. Walter, "Discrete Simulation of Power Law Noise", Proc. 1992 IEEE Freq. Contrl. Symp., pp. 274-283, May 1992.
- C.A. Greenhall, D.A. Howe and D.B Percival, “Total Variance, an Estimator of Long-Term Frequency Stability”, IEEE Trans. Ultrasonics, Ferroelectrics and Freq. Contrl., Vol. UFFC-46, No. 5, pp. 1183-1191, Sept. 1999.
Last Rev: 08/13/04